¿Te va a caer un rayo o no?
Merece la pena reflexionar sobre por qué necesitamos el concepto de probabilidades. Las cosas son o no son, ¿verdad? O bien nos caerá un rayo hoy, o bien no nos caerá. El problema es que no lo sabemos hasta que vivimos el día, lo que no nos ayuda en absoluto cuando tomamos nuestras decisiones por la mañana. El futuro no está ni mucho menos determinado, y podemos navegar mejor por él si comprendemos la probabilidad de los acontecimientos que podrían afectarnos.
Nuestra falta de información perfecta sobre el mundo da lugar a toda la teoría de la probabilidad, y a su utilidad. Ahora sabemos que el futuro es intrínsecamente imprevisible porque no se pueden conocer todas las variables y hasta el más pequeño error imaginable en nuestros datos desbarata rápidamente nuestras predicciones. Lo mejor que podemos hacer es estimar el futuro generando probabilidades realistas y útiles. ¿Y cómo lo hacemos?
La probabilidad está en todas partes, hasta en los mismos huesos del mundo. La maquinaria probabilística de nuestras mentes -la heurística rápida que hicieron tan famosa los psicólogos Daniel Kahneman y Amos Tversky- fue desarrollada por la especie humana en una época anterior a los ordenadores, las fábricas, el tráfico, los mandos intermedios y la bolsa. Nos sirvió en una época en la que la vida humana giraba en torno a la supervivencia, y aún nos sirve para ello.
Pero, ¿qué pasa hoy en día, una época en la que, para la mayoría de nosotros, la supervivencia no es tan importante? Queremos prosperar. Queremos competir y ganar. Sobre todo, queremos tomar buenas decisiones en sistemas sociales complejos que no formaban parte del mundo en el que nuestros cerebros evolucionaron su heurística (bastante racional).
Para ello, necesitamos añadir conscientemente una capa necesaria de conciencia de la probabilidad. ¿Qué es y cómo puedo utilizarla en mi beneficio?
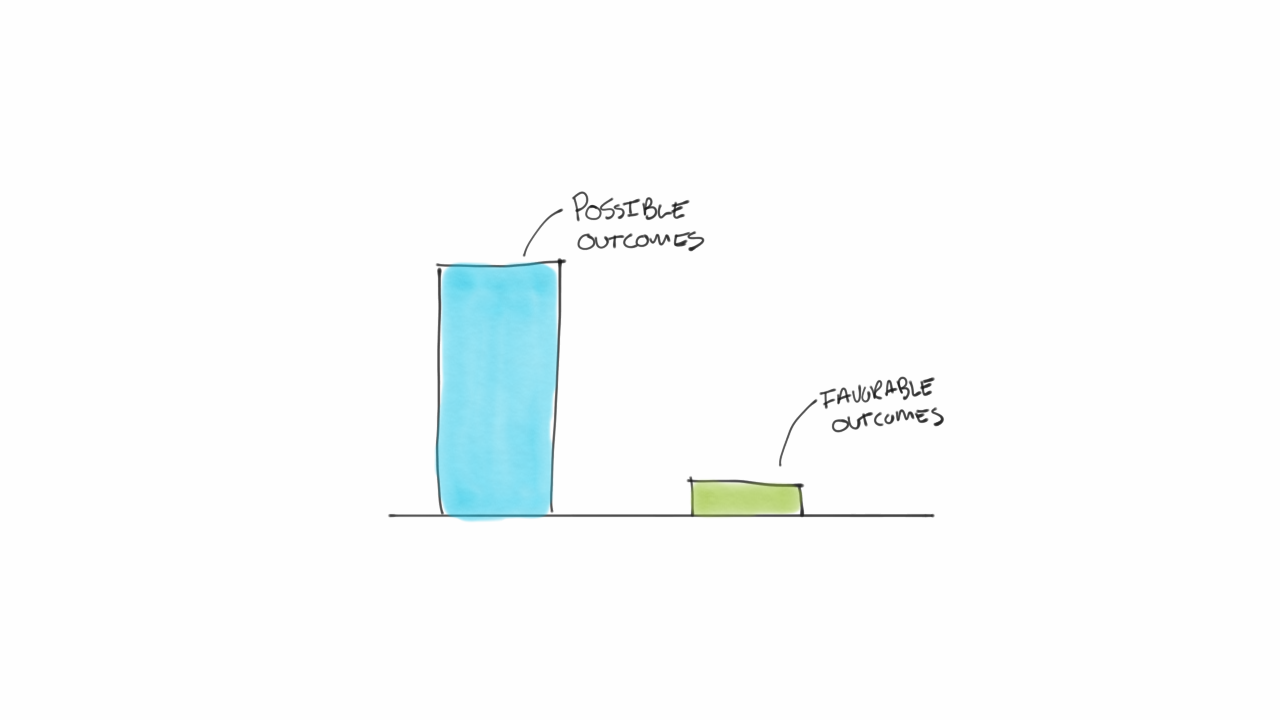
Hay tres aspectos importantes de la probabilidad que tenemos que explicar para que puedas integrarlos en tu pensamiento para entrar en el terreno de juego y mejorar tus posibilidades de atrapar la pelota:
-
- Pensamiento bayesiano,
- Curvas de cola gorda
- Asimetrías
Thomas Bayes y el pensamiento bayesiano: Bayes fue un ministro inglés de la primera mitad del siglo XVIII, cuya obra más famosa, “An Essay Toward Solving a Problem in the Doctrine of Chances” (Un ensayo para resolver un problema de la doctrina de las probabilidades) fue presentada a la Royal Society por su amigo Richard Price en 1763, dos años después de su muerte. El ensayo, la clave de lo que ahora conocemos como Teorema de Bayes, se refería a cómo debemos ajustar las probabilidades cuando nos encontramos con nuevos datos.
El núcleo del pensamiento bayesiano (o de la actualización bayesiana, como puede llamarse) es el siguiente: dado que tenemos una información limitada pero útil sobre el mundo, y que nos encontramos constantemente con nueva información, probablemente deberíamos tener en cuenta lo que ya sabemos cuando aprendemos algo nuevo. Tanto como sea posible. El pensamiento bayesiano nos permite utilizar toda la información previa relevante para tomar decisiones. Los estadísticos podrían llamarlo tasa base, teniendo en cuenta la información externa sobre situaciones pasadas como la que estás viviendo.
Considera el titular “Aumentan los apuñalamientos violentos”. Sin el pensamiento bayesiano, podrías sentir verdadero miedo porque tus posibilidades de ser víctima de una agresión o un asesinato son mayores que hace unos meses. Pero un enfoque bayesiano te hará poner esta información en el contexto de lo que ya sabes sobre la delincuencia violenta.
Sabes que la delincuencia violenta ha disminuido hasta alcanzar sus índices más bajos en décadas. Tu ciudad es más segura ahora de lo que ha sido desde que comenzó esta medición. Digamos que tu probabilidad de ser víctima de un apuñalamiento el año pasado fue de una entre 10.000, es decir, del 0,01%. El artículo afirma, con exactitud, que los delitos violentos se han duplicado. Ahora son dos de cada 10.000, o el 0,02%. ¿Merece la pena preocuparse mucho por ello? La información previa aquí es clave. Cuando la tenemos en cuenta, nos damos cuenta de que nuestra seguridad no se ha visto realmente comprometida.
Por el contrario, si observamos las estadísticas de la diabetes en Estados Unidos, la aplicación del conocimiento previo nos llevaría a una conclusión diferente. En este caso, un análisis bayesiano indica que debes preocuparte. En 1958, el 0,93% de la población estaba diagnosticada de diabetes. En 2015 era el 7,4%. Si observas los años intermedios, el aumento del diagnóstico de diabetes es constante, no un pico. Así que los datos relevantes anteriores, o priores, indican una tendencia preocupante.
Es importante recordar que los priores son en sí mismos estimaciones de probabilidad. Para cada bit de conocimiento previo, no lo estás poniendo en una estructura binaria, diciendo que es cierto o no. Le estás asignando una probabilidad de ser verdadero. Por tanto, no puedes dejar que tus conocimientos previos se interpongan en el procesamiento de los nuevos conocimientos. En términos bayesianos, esto se denomina razón de verosimilitud o factor de Bayes. Cualquier información nueva que encuentres y que ponga en tela de juicio una teoría a priori simplemente significa que la probabilidad de que esa teoría a priori sea cierta puede reducirse. Con el tiempo, algunos prioritarios se sustituyen por completo. Se trata de un ciclo continuo de desafío y validación de lo que crees saber. Cuando se toman decisiones inciertas, casi siempre es un error no preguntarse: ¿Cuáles son las prioridades relevantes? ¿Qué puedo saber ya que pueda utilizar para comprender mejor la realidad de la situación?
Ahora tenemos que mirar las curvas de cola gorda: Muchos de nosotros estamos familiarizados con la curva de campana, esa bonita y simétrica onda que capta la frecuencia relativa de muchas cosas, desde la altura hasta las notas de los exámenes. La curva de campana es estupenda porque es fácil de entender y de utilizar. Su nombre técnico es “distribución normal”. Si sabemos que estamos en una situación de curva de campana, podemos identificar rápidamente nuestros parámetros y planificar los resultados más probables.
Las curvas de cola gorda son diferentes. Echa un vistazo.
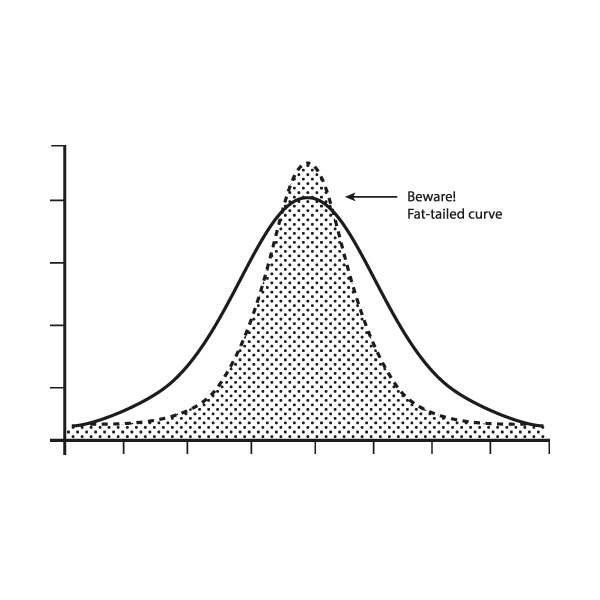
A primera vista parecen bastante similares. Los resultados comunes se agrupan, creando una ola. La diferencia está en las colas. En una curva de campana, los extremos son predecibles. Sólo puede haber una determinada desviación de la media. En una curva de cola gruesa no hay un límite real para los sucesos extremos. Cuantos más sucesos extremos sean posibles, más largas serán las colas de la curva.
Cualquier suceso extremo sigue siendo improbable, pero el gran número de opciones significa que no podemos confiar en que los resultados más comunes representen la media. Cuantos más sucesos extremos sean posibles, mayor será la probabilidad de que uno de ellos ocurra. Definitivamente, van a ocurrir cosas locas, y no tenemos forma de identificar cuándo.
Piénsalo así. En una situación del tipo de la curva de campana, como la que muestra la distribución de la altura o el peso en una población humana, hay valores atípicos en el espectro de posibilidades, pero los valores atípicos tienen un alcance bastante bien definido. Nunca conocerás a un hombre que tenga diez veces la talla media. Pero en una curva con colas gordas, como la de la riqueza, la tendencia central no funciona igual. Puedes conocer regularmente a personas que son diez, cien o diez mil veces más ricas que la persona media. Ese es un tipo de mundo muy diferente. Volvamos a abordar el ejemplo de los riesgos de violencia que comentamos en relación con el pensamiento bayesiano.
Supón que te dicen que tienes más riesgo de resbalar en las escaleras y abrirte la cabeza que de ser asesinado por un terrorista. Las estadísticas, los antecedentes, parecen respaldarlo: 1.000 personas se resbalaron en las escaleras y murieron el año pasado en tu país y sólo 500 murieron a causa del terrorismo. ¿Deberías estar más preocupado por las escaleras o por los acontecimientos terroristas?
Algunos utilizan ejemplos como éste para demostrar que el riesgo terrorista es bajo: dado que el pasado reciente muestra muy pocas muertes, ¿por qué preocuparse? [1] El problema está en las colas gordas: El riesgo de violencia terrorista se parece más a la riqueza, mientras que las muertes por caída de escaleras se parecen más a la altura y al peso. En los próximos diez años, ¿cuántos sucesos son posibles? ¿Cómo de gorda es la cola? Lo importante no es sentarse a imaginar todos los escenarios posibles de la cola (por definición, es imposible), sino enfrentarse a los dominios de cola gorda de la forma correcta: posicionándonos para sobrevivir o incluso beneficiarnos del futuro salvajemente imprevisible, siendo los únicos que piensan correctamente y planifican para un mundo que no comprendemos del todo.
Asimetrías: Por último, tienes que pensar en algo que podríamos llamar “metaprobabilidad”: la probabilidad de que tus estimaciones de probabilidad sean buenas.
Este concepto tan incomprendido tiene que ver con las asimetrías. Si observas los lanzamientos de acciones bien pulidos que hacen los inversores profesionales, casi siempre que se presenta una idea, el inversor mira a su público a los ojos y afirma que cree que va a conseguir una tasa de rendimiento del 20% al 40% anual, si no más. Sin embargo, excesivamente pocos de ellos llegan a alcanzar esa marca, y no es porque no tengan ningún ganador. Es porque se equivocan mucho. Sobreestiman sistemáticamente su confianza en sus estimaciones probabilísticas. (Como referencia, el mercado de valores en general no ha devuelto más del 7% al 8% anual en Estados Unidos durante un largo periodo, antes de las comisiones).
Otra asimetría común es la capacidad de la gente para estimar el efecto del tráfico en el tiempo de viaje. ¿Con qué frecuencia sales “a tiempo” y llegas un 20% antes? ¿Casi nunca? ¿Con qué frecuencia sales “a tiempo” y llegas un 20% tarde? ¿Todo el tiempo? Exactamente. Tus errores de estimación son asimétricos, se inclinan en una sola dirección. Esto suele ocurrir en la toma de decisiones probabilísticas.[2] Muchas más estimaciones de probabilidad se equivocan en el lado “demasiado optimista” que en el lado “poco optimista”. Rara vez leerás sobre un inversor que se propusiera obtener un 25% de rentabilidad anual y que posteriormente ganara un 40% durante un largo periodo de tiempo. Puedes lanzar un dardo en el Wall Street Journal y acertar los nombres de muchos inversores que aspiran a un 25% anual con cada inversión y acaban más cerca del 10%.
El mundo de los espías
Los espías de éxito son muy buenos en el pensamiento probabilístico. Las situaciones de supervivencia de alto riesgo tienden a hacernos evaluar nuestro entorno con el menor sesgo posible.
Cuando Vera Atkins era la segunda al mando de la unidad francesa del Special Operations Executive (SOE), una organización de inteligencia británica que dependía directamente de Winston Churchill durante la Segunda Guerra Mundial[3], tuvo que tomar cientos de decisiones calculando la exactitud probable de una información intrínsecamente poco fiable.
Atkins era responsable del reclutamiento y despliegue de agentes británicos en la Francia ocupada. Tenía que decidir quién podía hacer el trabajo y dónde estaban las mejores fuentes de información. Eran decisiones literalmente de vida o muerte, y todas se basaban en el pensamiento probabilístico.
En primer lugar, ¿cómo se elige a un espía? No todo el mundo puede ir de incógnito en situaciones de gran tensión y hacer los contactos necesarios para reunir información. El resultado del fracaso en Francia en la Segunda Guerra Mundial no fue el despido, sino la muerte. ¿Qué factores de personalidad y experiencia demuestran que una persona es adecuada para el trabajo? Incluso hoy en día, con los avances en psicología, interrogatorios y polígrafos, sigue siendo una cuestión de juicio.
Para Vera Atkins, en la década de 1940, era un proceso que consistía en asignar peso a los distintos factores y llegar a una evaluación probabilística de quién tenía una posibilidad decente de éxito. ¿Quién hablaba francés? ¿Quién tenía confianza en sí mismo? ¿Quién estaba demasiado atado a la familia? ¿Quién tenía capacidad para resolver problemas? Desde el reclutamiento hasta el despliegue, su desarrollo de cada espía era una serie de estimaciones educadas continuamente actualizadas.
Conseguir que un agente de inteligencia esté listo para partir es sólo la mitad de la batalla. ¿Adónde lo envías? Si tu información fuera tan grande que supieras exactamente a dónde ir, probablemente no necesitarías una misión de inteligencia. Elegir un objetivo es otro ejercicio de pensamiento probabilístico. Tienes que evaluar la fiabilidad de la información que tienes y de las redes que has creado.
La inteligencia no es una prueba. No hay cadena de mando ni garantía de autenticidad. El material que salía de la Francia ocupada por los alemanes estaba al nivel de fotografías granuladas, notas manuscritas que pasaban por muchas manos de vuelta al cuartel general, y mensajes inalámbricos no verificables enviados rápidamente, a veces de forma esporádica, y con el operador sometido a un estrés increíble.
Al decidir qué utilizar, Atkins tuvo que considerar la relevancia, la calidad y la oportunidad de la información que tenía. También tuvo que tomar decisiones basadas no sólo en lo que había ocurrido, sino en lo que posiblemente podría ocurrir. Tratar de prepararse para cualquier eventualidad significa que los espías nunca saldrían de casa, pero deben prepararse de algún modo para una buena parte de lo inesperado. Al fin y al cabo, sus trabajos se ejecutan a menudo en entornos muy volátiles y dinámicos.
Las mujeres y los hombres que Atkins envió a Francia trabajaban en tres ocupaciones principales: los organizadores se encargaban de reclutar a la población local, desarrollar la red e identificar los objetivos de sabotaje; los mensajeros trasladaban la información por todo el país, conectando a las personas y las redes para coordinar las actividades; y los operadores inalámbricos tenían que instalar equipos de comunicaciones pesados, disfrazarlos, sacar la información del país y estar preparados para moverse en cualquier momento.
Todos estos trabajos eran peligrosos. El alcance total de las amenazas nunca fue completamente identificable. Había tantas cosas que podían salir mal, tantas posibilidades de descubrimiento o traición, que era imposible planificarlas todas. La esperanza de vida media en Francia de uno de los operadores inalámbricos de Atkins era de seis semanas.
Por último, las cifras sugieren una asimetría en la estimación de la probabilidad de éxito de cada agente individual. De los 400 agentes que Atkins envió a Francia, 100 fueron capturados y asesinados. Esto no pretende juzgar sus habilidades o su inteligencia. El pensamiento probabilístico sólo te puede llevar al terreno de juego. No garantiza el 100% de éxito. No hay duda de que Atkins se basó en gran medida en el pensamiento probabilístico para guiar sus decisiones en la desafiante búsqueda de interrumpir las operaciones alemanas en Francia durante la Segunda Guerra Mundial.
Es difícil evaluar el éxito de una carrera de espionaje, porque es un trabajo que conlleva muchas pérdidas. Atkins tuvo un gran éxito, ya que su red llevó a cabo valiosos sabotajes para apoyar la causa aliada durante la guerra, pero la pérdida de vidas fue importante.
Conclusión
Pensar con éxito en tonos de probabilidad significa identificar a grandes rasgos lo que importa, tener una idea de las probabilidades, hacer una comprobación de nuestras suposiciones y luego tomar una decisión. Podemos actuar con un mayor nivel de certeza en situaciones complejas e imprevisibles.
Nunca podemos conocer el futuro con precisión exacta. El pensamiento probabilístico es una herramienta extremadamente útil para evaluar cómo será el mundo con toda probabilidad, de modo que podamos elaborar una estrategia eficaz.
Referencias:
[1] Taleb, Nassim Nicholas. Antifrágil. Nueva York: Random House, 2012.
[2] Bernstein, Peter L. Contra los dioses: La notable historia del riesgo. Nueva York: John Wiley and Sons, 1996. (Este libro incluye un excelente debate en el capítulo 13 sobre la idea del alcance de los acontecimientos en el pasado como relevante para averiguar la probabilidad de los acontecimientos en el futuro, basándose en el trabajo de Frank Knight y John Maynard Keynes).
[3] Helm, Sarah. Una vida en secretos: La historia de Vera Atkins y los agentes perdidos del SOE. Londres: Abacus, 2005.




